Caratterizzazione numerico-sperimentale delle guarnizioni ed elastomeri

Guarnizioni ed elastomeri sono componenti critici utilizzati in una vasta gamma di applicazioni industriali, dall'automotive all'aerospace, dall'elettronica alla produzione di energia. La loro capacità di esprimere capacità sigillanti, smorzamento delle vibrazioni e resistenza chimica è fondamentale per garantire prestazioni affidabili e durature dei sistemi in cui vengono impiegati. Tuttavia, la complessità delle interazioni tra questi materiali polimerici e l'ambiente circostante richiede un'approfondita caratterizzazione numerico-sperimentale al fine di comprenderne le proprietà e le prestazioni in modo accurato e affidabile. 

Caratterizzazione multifisica degli elastomeri

La caratterizzazione delle guarnizioni ed elastomeri richiede un approccio multidisciplinare che coinvolge la scienza dei materiali, la chimica, la fisica e l'ingegneria. Sono necessari varie tipologie di test per valutare una serie di proprietà chiave, tra cui la resistenza meccanica, la resilienza agli agenti chimici, la resistenza all'invecchiamento e la stabilità termica.

Tra i test fondamentali per la caratterizzazione degli elastomeri ci sono il test di trazione, di compressione, di taglio ed il test volumetrico. Queste informazioni sono cruciali per determinare la rigidezza e resistenza dell'elastomero, che da un punto di vista ingegneristico si esprime con una caratteristica iperelastica, ovvero elastica non lineare.

Tuttavia, la caratterizzazione delle guarnizioni ed elastomeri non si limita solo a test meccanici e chimici. L'analisi termica, ad esempio, è fondamentale per valutare la stabilità termica e l'intervallo di temperature di esercizio dei materiali elastomerici. L'analisi spettroscopica può essere utilizzata per identificare le strutture chimiche presenti nel materiale e valutarne la composizione.

Il valore aggiunto della simulazione numerica nello studio delle guarnizioni

La simulazione numerica riveste un ruolo fondamentale nella caratterizzazione degli elastomeri, offrendo un approccio complementare ai test sperimentali tradizionali. Questo approccio computazionale consente di ridurre il numero di test fisici richiesti, ottimizzando il processo di caratterizzazione e riducendo i costi associati. Inoltre, la simulazione numerica consente di esplorare una vasta gamma di condizioni di carico e ambientali in modo rapido ed efficiente.

Un aspetto particolarmente vantaggioso della simulazione numerica è la capacità di modellare geometrie complesse e riprodurre virtualmente i problemi di insersione della guarnizione. Mentre i test sperimentali spesso richiedono la costruzione di prototipi fisici, la simulazione numerica consente di creare modelli virtuali in cui è possibile variare facilmente le dimensioni, la forma e la 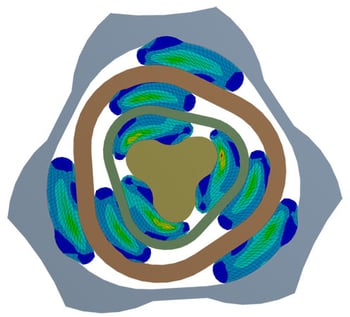geometria delle guarnizioni ed elastomeri. Ciò consente di studiare il comportamento del materiale in condizioni realistiche e di valutare l'effetto di diverse geometrie sulla performance.

Inoltre, la simulazione numerica può aiutare a predire l'efficacia delle guarnizioni in termini di sigillatura. Sono possibili analisi di contatto tra le superfici delle guarnizioni e i componenti adiacenti, consentendo di valutare la distribuzione delle pressioni, le forze di tenuta e le perdite in base ai fenomeni di attrito. Ciò consente di ottimizzare il design delle guarnizioni ed elastomeri per massimizzare la tenuta e minimizzare eventuali problemi di tenuta.

Modelli matematici polinomiali per caratterizzare gli elastomeri

Nello sviluppo di un modello CAE, i modelli iperelastici polinomiali consentono di riprodurre in modo affidabile il comportamento iperelastico degli elastomeri. Questi modelli utilizzano equazioni polinomiali per descrivere la relazione tra lo sforzo e la deformazione nel materiale el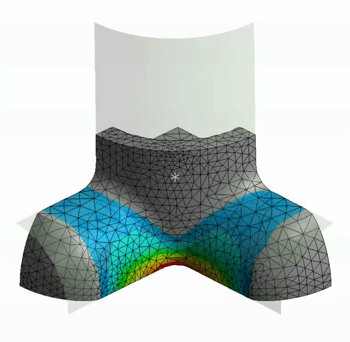astomerico, tenendo conto delle non linearità presenti nel comportamento intrinseco della guarnizione. I coefficienti polinomiali vengono determinati tramite test sperimentali o dati forniti dal produttore del materiale, sfruttando le tecniche di material data fitting. I codici FEM offrono diversi modelli polinomiali per la caratterizzazione dei materiali elastomerici iperelastici. Alcuni dei principali modelli sono:

1. Modello Mooney-Rivlin: è un modello polinomiale di secondo ordine che descrive il comportamento dei materiali elastomerici. Utilizza 2, 3, 5 o 9 parametri costanti per descrivere le proprietà di tensione-deformazione del materiale.
2. Modello Ogden: è un modello polinomiale (di 1°, 2°, 3° o n° ordine) di tipo generale che può essere utilizzato per rappresentare il comportamento elastico non lineare dei materiali elastomerici. Utilizza più parametri costanti per caratterizzare le proprietà dei materiali in base a diverse deformazioni.
3. Modello Yeoh: È un modello polinomiale (di 1°, 2°, 3° o n° ordine) che viene spesso utilizzato per caratterizzare il comportamento dei materiali elastomerici in un'ampia gamma di deformazioni. Richiede l'utilizzo di tre o più parametri costanti per rappresentare le proprietà di tensione-deformazione.
4. Modello Arruda-Boyce: È un modello polinomiale di tipo generale che tiene conto delle non linearità geometriche e delle deformazioni finite. Utilizza un'equazione polinomiale per rappresentare le proprietà di tensione-deformazione e richiede la specifica di diversi parametri costanti.
   
   

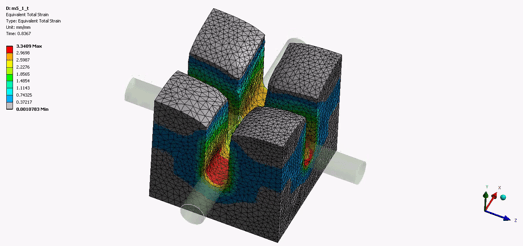
Tecniche di remeshing automatico per simulare l’inserimento delle guarnizioni

Infine, per riprodurre le grandi deformazioni tipiche di un elastomero, è raccomandato l’utilizzo della tecnica NonLinear ADaptivity (NLAD). Di seguito si riportano le caratteristiche e vantaggi principali:

1. Accuratezza: la tecnica NLAD consente di ottenere risultati più accurati e affidabili nello studio del comportamento degli elastomeri. Durante l'analisi, la mesh viene adattata automaticamente in modo da concentrare i punti di calcolo dove sono presenti sollecitazioni elevate o deformazioni significative. Ciò permette di catturare in modo più preciso le regioni critiche del materiale elastomerico, migliorando la risoluzione e riducendo gli errori di discretizzazione.
2. Efficienza computazionale: utilizzando la tecnica NLAD, è possibile ridurre il numero complessivo di punti di calcolo necessari per ottenere risultati accurati. La tecnica adatta la mesh solo nelle regioni di interesse, riducendo il carico computazionale complessivo dell'analisi. Ciò porta a tempi di calcolo più rapidi e a un utilizzo più efficiente delle risorse computazionali.
3. Gestione dei problemi di localizzazione degli stress: gli elastomeri possono mostrare comportamenti altamente non lineari e localizzati, come la formazione di zone di concentrazione degli stress. La tecnica NLAD permette di affrontare questi problemi, adattando automaticamente la mesh per catturare tali zone di alta sollecitazione. Ciò consente di ottenere una valutazione accurata delle regioni critiche in cui si verificano danni o deformazioni localizzate.
4. Flessibilità nello studio di geometrie complesse: la tecnica NLAD è particolarmente vantaggiosa quando si studiano geometrie complesse o dettagliate come guarnizioni o giunzioni elastomeriche. La mesh viene adattata in modo da concentrare i punti di calcolo nelle zone di interesse, consentendo di ottenere una rappresentazione dettagliata e accurata delle caratteristiche geometriche complesse. Questo è particolarmente importante per valutare le tensioni localizzate, le deformazioni e le interazioni tra l'elastomero e le superfici di contatto adiacenti.

Se ti interessa avere maggiori informazioni su questa metodologia e scoprire i vantaggi che la tua azienda avrebbe nell'integrarla all'interno dei suoi processi di progettazione e produzione, contattaci, uno dei nostri esperti risponderà a tutte le tue domande.