Metodi numerici per la simulazione in ingegneria

I problemi ingegneristici possono essere risolti con diverse metodologie, e la risoluzione con metodi numerici per la simulazione fornisce una serie di punti positivi che contribuiscono a una migliore comprensione dei fenomeni con un buon equilibrio tra tempi, costi e qualità.

I metodi numerici sono applicazioni di algoritmi che consentono di formulare e risolvere problemi matematici utilizzando operazioni aritmetiche meno complesse. Questi sono noti anche come metodi indiretti. L'analisi numerica idealizza e progetta metodi per "passare" in modo efficiente le soluzioni a problemi espressi matematicamente. L'obiettivo principale dell'analisi numerica è trovare soluzioni "approssimate" a problemi complessi.

Un algoritmo è un gruppo finito di operazioni organizzate e ordinate che consente di risolvere un determinato problema. Si tratta di una serie di istruzioni o regole stabilite che, attraverso una successione di passaggi, permettono di approssimare il risultato reale.

L'analisi numerica è lo studio di algoritmi che cercano di ottenere risultati numerici di problemi provenienti dalle più diverse aree della conoscenza umana, modellati matematicamente. In generale, gli algoritmi dei metodi numerici si dividono in diretti, ricorsivi e iterativi. Ad esempio, le soluzioni iterative prevedono una successione di passi che convergono o meno al valore approssimato della soluzione esatta. L'obiettivo dell'analisi numerica è trovare sequenze che approssimano valori esatti con un numero minimo di operazioni elementari.

Sebbene l'analisi numerica sia stata concepita prima dei computer, l'argomento è attualmente legato a un approccio interdisciplinare tra matematica e tecnologia dell'informazione. Viene spesso citato anche nell'ambito del calcolo numerico.

Le descrizioni qui presentate sono semplificate e mirano a far comprendere al lettore i fondamenti dei metodi, le loro differenze e le principali applicazioni. Essi sono:

Metodo degli elementi finiti (FEM)

Il metodo FEM è un metodo numerico per risolvere problemi di ingegneria e fisica matematica. È applicabile a diverse discipline ingegneristiche, come quelle strutturali, termiche ed elettromagnetiche.

Si tratta di un metodo numerico che supera i limiti dei problemi risolvibili con soluzioni analitiche ed è adatto ad affrontare problemi con geometrie, carichi e proprietà dei materiali complessi.

Consideriamo un dominio, ad esempio la geometria dell'oggetto di studio. Questo dominio sarà considerato continuo. Questo continuum è suddiviso in un numero discreto di piccoli corpi con una forma specifica, chiamati elementi finiti, e interconnessi da punti comuni chiamati punti nodali o nodi.

La procedura di discretizzazione (la divisione del continuo in parti più piccole), di equazione e di calcolo è adatta alla programmazione e al successivo utilizzo su computer, il che l'ha resa molto popolare e utile per diversi settori. In sintesi, la suddivisione della geometria in elementi finiti permette di risolvere un problema complesso suddividendolo in problemi più semplici, consentendo al computer di svolgere questi compiti in modo efficiente.

Il metodo degli elementi finiti risolve diversi problemi che vengono equiparati e ridotti a sistemi di equazioni differenziali. Ad esempio, quando si considera il calcolo strutturale, si ricava un'equazione, detta equazione del moto, che riassume l'equilibrio tra le forze interne di una struttura (forza inerziale, forza di smorzamento e forza elastica) e una forza esterna. Se il problema è statico o quasi statico, si considera solo l'equilibrio tra forze interne elastiche e forze esterne.

Scoprite come Ansys Mechanical aiuta gli ingegneri a risolvere in modo efficiente problemi di progettazione complessi utilizzando l'analisi a elementi finiti.

Esaminiamo, per capire meglio, un semplice problema statico, i cui fondamenti saranno applicati per la soluzione con il metodo degli elementi finiti.

Nel 1660 Robert Hooke osservò e descrisse la cosiddetta legge dell'elasticità, che porta il suo nome: legge di Hooke. Descrive che il legame tra la variazione della tensione e l'estensione in una molla è lineare.

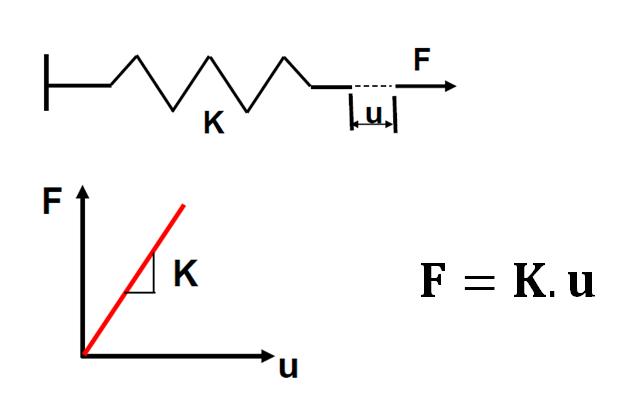Figura 1: Relazione (legge di Hooke) tra sollecitazione esterna (F), rigidità (K) e spostamento (u). K.u rappresenta lo sforzo interno.

In un problema in cui la geometria è più complessa di una molla lineare, la geometria viene discretizzata e da ogni componente (elemento) della struttura discretizzata e dalla conoscenza delle proprietà dei materiali costituenti, si ottiene la rigidità dell'elemento. Gli elementi sono collegati da vertici, chiamati nodi, che formano la struttura continua discretizzata.

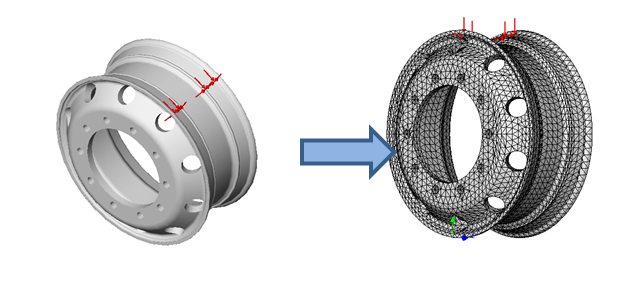
Matematicamente, con la rigidità di ogni elemento e conoscendo i movimenti di ogni nodo, chiamati gradi di libertà (GDL) o, in inglese, Degrees of Freedom (DOF), si forma una matrice di rigidità che rappresenta la rigidità della struttura a geometria complessa.

Nella figura 2, che rappresenta la rigidità globale, N è il numero dei gradi di libertà.

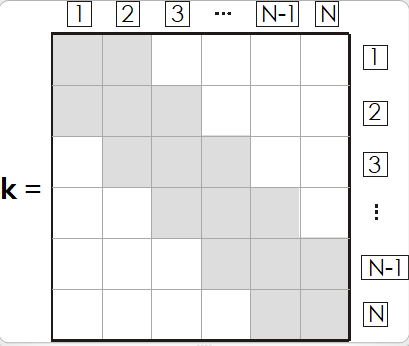
Figura 2: Matrice di rigidità globale della struttura.

In questo modo, la relazione tra forza esterna, rigidità e spostamento può essere scritta in forma di matrice. Dove:

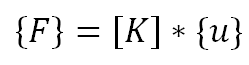
{ F } - vettore delle forze esterne

[ K ] - rigidità complessiva

{ u } - vettore degli spostamenti

In questo problema, gli spostamenti sono i valori sconosciuti (le incognite) del problema, quindi si utilizza una procedura di soluzione del sistema di equazioni (un solutore) e si calcolano gli spostamenti di ciascun nodo. Dagli spostamenti, si ottengono le sollecitazioni, le deformazioni, le reazioni di supporto e altre risposte che gli analisti possono ricercare.

Metodo degli elementi discreti (DEM)

Un metodo a elementi discreti o metodo a elementi distinti (DEM) è, di fatto, un metodo appartenente a una famiglia di metodi per calcolare il movimento e l'effetto di un gran numero di piccole particelle (discrete).

Il metodo degli elementi discreti è legato alla dinamica molecolare, ma si differenzia per l'inclusione di gradi di libertà rotazionali (moti), per il contatto tra gli elementi discreti e per le geometrie spesso complesse utilizzate per definirli.

Esistono diversi rami della famiglia, come il metodo degli elementi discreti proposto da Cundall nel 1971, il metodo degli elementi discreti generalizzato (Willians, Hocking e Mustoe) nel 1985, il metodo delle deformazioni discontinue (Shi, 1992) e il metodo degli elementi finiti discreti sviluppato contemporaneamente da diversi team (ad esempio Munjiza e Owen), il metodo delle deformazioni discontinue (Shi, 1992) e il metodo degli elementi finiti discreti sviluppato contemporaneamente da diversi team (ad esempio Munjiza e Owen). Il metodo generale è stato originariamente sviluppato da Peter Cundall nel 1971 per risolvere problemi di geomeccanica (rocce).

Ansys Rocky utilizza il metodo degli elementi discreti per le simulazioni. Per saperne di più.

In breve, la simulazione con il DEM viene avviata generando un modello che determina l'orientamento spaziale e la velocità iniziale di tutte le particelle. Le forze che agiscono su ciascuna particella sono calcolate in base alle condizioni iniziali e alle leggi fisiche (meccanica newtoniana) e di contatto pertinenti. Il risultato, una nuova disposizione delle particelle, può essere visualizzato in un software di visualizzazione progettato a questo scopo (un post-processore).

Il DEM è attualmente considerato un metodo di analisi efficace per la simulazione di problemi ingegneristici che coinvolgono discretizzazioni e materiali discontinui, come il flusso granulare e la geomeccanica. I recenti progressi nella capacità di risolvere grandi sistemi di equazioni, grazie allo sviluppo e alla riduzione dei prezzi dei computer, all'elaborazione parallela e agli algoritmi numerici, consentono di risolvere problemi computazionalmente intensivi con un gran numero di particelle.

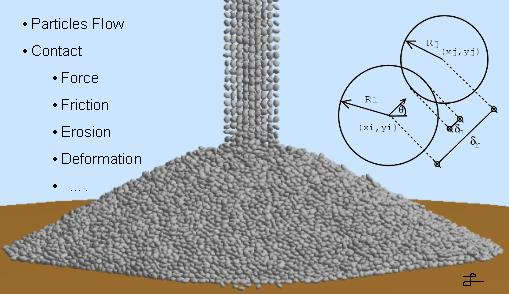
Figura 3: Rappresentazione del contatto tra particelle (forma sferica).

La premessa fondamentale del metodo è che il materiale è costituito da particelle discrete e separate. Queste particelle possono avere forme e proprietà diverse, ad esempio: grani, pietre, sabbia, toner, pillole e zucchero.

I settori che tipicamente utilizzano il DEM sono: agricolo, alimentare, chimico, minerario, farmaceutico, metallurgia delle polveri, ingegneria civile, industria petrolifera e del gas, lavorazione dei minerali.

Metodo del volume finito (FVM)

Il metodo dei volumi finiti (FVM) è stato introdotto negli anni '70 da McDonald, MacCormack e Paullay ed è stato storicamente il metodo preferito da scienziati e ingegneri che si occupano di meccanica dei fluidi, anche se l'FVM non è limitato alla risoluzione di problemi di meccanica dei fluidi.

Attualmente, il metodo dei volumi finiti viene utilizzato per risolvere problemi di meccanica dei fluidi, alcuni dei quali considerati complessi come quelli che coinvolgono flussi multifase, reattivi o fortemente turbolenti. In pratica, la FVM si è dimostrata il metodo più efficace per calcolare e risolvere diversi problemi di meccanica dei fluidi.

Per risolvere i problemi di meccanica dei fluidi, Ansys Fluent è lo strumento giusto per innovare e ottimizzare le prestazioni dei vostri prodotti. Apprendi.

Si consideri che nel metodo dei volumi finiti vi è una decomposizione (discretizzazione) del dominio continuo in piccoli volumi, detti volumi di controllo (CV), dove le variabili sono calcolate e memorizzate nei nodi o al centro del volume. Questi volumi di controllo sono collegati tra loro da questi nodi e definiscono una griglia numerica chiamata mesh, illustrata nella Figura 1. La Figura 2 mostra i nodi ai vertici e al centro dei volumi.

Nel metodo dei volumi finiti si utilizza l'idea dell'osservazione di Eulero, cioè il materiale scorre attraverso un volume di controllo fisso. Dai valori calcolati nei nodi e nei centri dei volumi di controllo si ottiene una soluzione che viene trasportata al resto del dominio.

Figura 4: Maglie di superficie colorate in base al rapporto d'aspetto delle celle. Disponibile all'indirizzo https://blog.pointwise.com.

I principi di conservazione della massa, del momento (quantità di moto) e dell'energia, sono alla base della modellazione matematica nel Metodo dei Volumi Finiti per la meccanica del continuo. Per definizione, questi principi sono rispettati dalle equazioni ottenute dalla discretizzazione del continuo effettuata con questo metodo. In generale, il VFM prevede le seguenti fasi:

• Decomporre il dominio in volumi di controllo

• Formulare le equazioni integrali di conservazione per ogni volume di controllo
• Approssimare numericamente gli integrali
• Approssimare i valori delle variabili sulle facce e le derivate con le informazioni delle variabili nodali
• Impostare e risolvere il sistema algebrico ottenuto

Il sistema di equazioni viene risolto e si ottengono risposte quali pressione, temperatura e velocità. Si noti che si tratta di una soluzione numerica approssimativa. Un aspetto fondamentale degli algoritmi di soluzione è il processo di decomposizione delle matrici, per il quale sono state sviluppate diverse tecniche per aumentare l'efficienza dell'uso delle risorse computazionali e la velocità di ottenimento dei risultati.

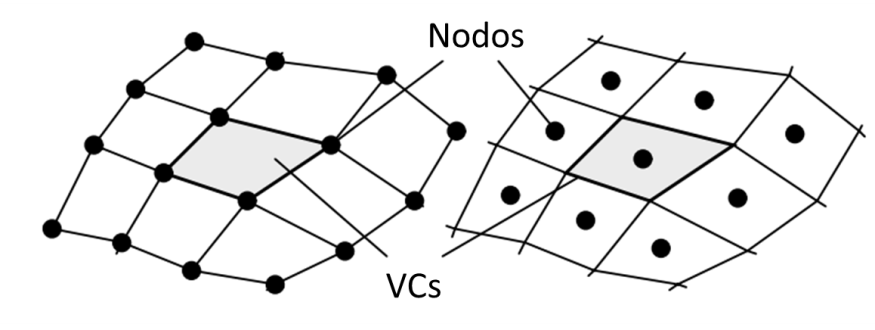Figura 5: I Nodi ai vertici dei VC (sinistra) e nodi al centro dei VC (destra) per una griglia quadrilatera.

Altri metodi numerici utilizzati per risolvere problemi di ingegneria:

Metodo degli Elementi al Contorno (BEM)

Il Boundary Element Method (BEM) è un metodo di calcolo per la soluzione di sistemi di equazioni differenziali, formulate in forma integrale. Viene applicata in molte aree dell'ingegneria, come la meccanica dei fluidi, l'acustica, l'elettromagnetismo e la meccanica delle fratture.

Nel BEM il contorno del dominio oggetto di studio viene discretizzato (suddiviso in elementi). Questo, in molti casi, riduce drasticamente le dimensioni del problema, oltre a semplificare l'implementazione dei preprocessori (generatori di geometrie e mesh). Una volta trovata la soluzione al contorno, nella fase di post-elaborazione, le equazioni integrali vengono nuovamente utilizzate per calcolare numericamente la soluzione in qualsiasi punto del dominio racchiuso dal contorno.

Metodo delle differenze finite (FDM)

In matematica, i metodi alle differenze finite (FDM) sono metodi numerici per risolvere le equazioni differenziali approssimandole con equazioni alle differenze, in cui le differenze finite approssimano le derivate. I FDM sono quindi metodi di discretizzazione.  Il metodo delle differenze finite si basa sulla discretizzazione di una funzione su una griglia.

Metodo Lattice-Boltzmann

Il Lattice-Boltzmann è spesso considerato un risolutore numerico dell'equazione di Boltzmann. L'equazione di Boltzmann è l'analogo dell'equazione di Navier-Stokes a livello molecolare, dove si descrive la dinamica spazio-temporale di una grandezza statistica chiamata funzione di distribuzione di probabilità, definita nello spazio delle fasi a sei dimensioni. Il numero di fenomeni fisici coperti dal modello a questo livello di descrizione molecolare è maggiore rispetto al livello idrodinamico dell'equazione di Navier-Stokes.

La simulazione al computer utilizza questi metodi numerici in diversi settori per aiutare gli ingegneri a risolvere i problemi. Per applicare simulazioni alla vostra azienda, contattate ESSS.

[IMMAGINE CTA: Rivoluzionate i vostri progetti con le simulazioni Ansys. Richiedi un preventivo]